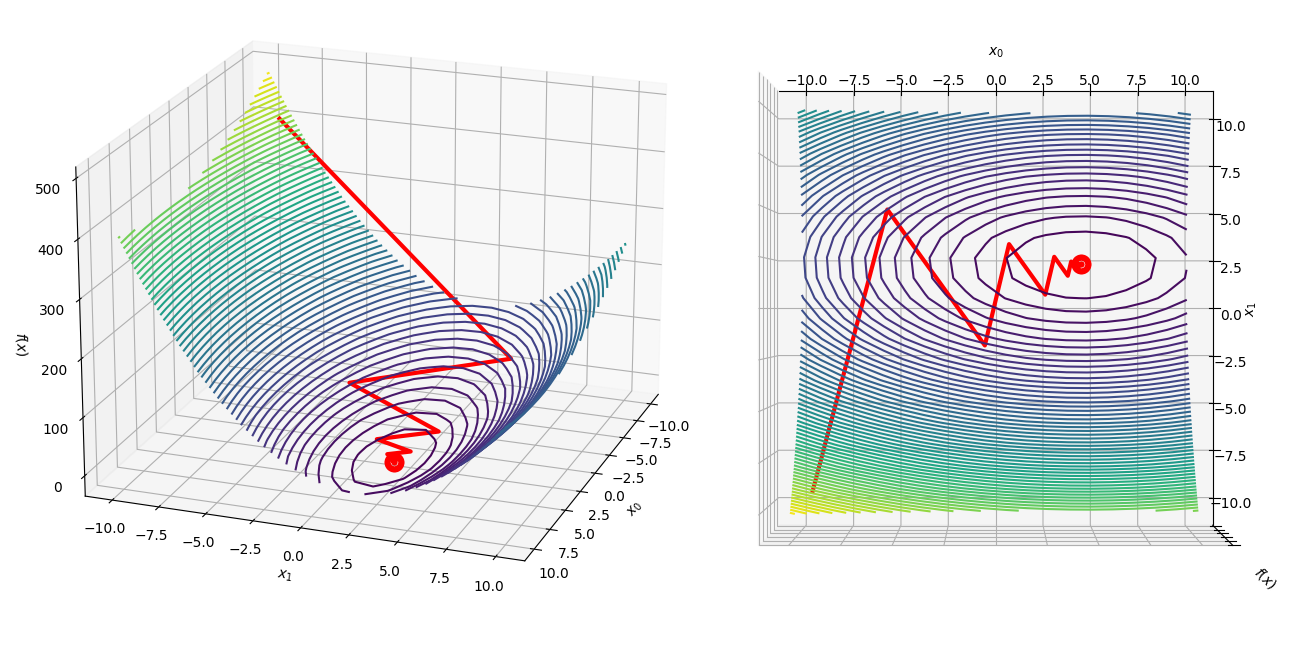
optimization - How to show that the method of steepest descent does not converge in a finite number of steps? - Mathematics Stack Exchange
Descrição
I have a function,
$$f(\mathbf{x})=x_1^2+4x_2^2-4x_1-8x_2,$$
which can also be expressed as
$$f(\mathbf{x})=(x_1-2)^2+4(x_2-1)^2-8.$$
I've deduced the minimizer $\mathbf{x^*}$ as $(2,1)$ with $f^*
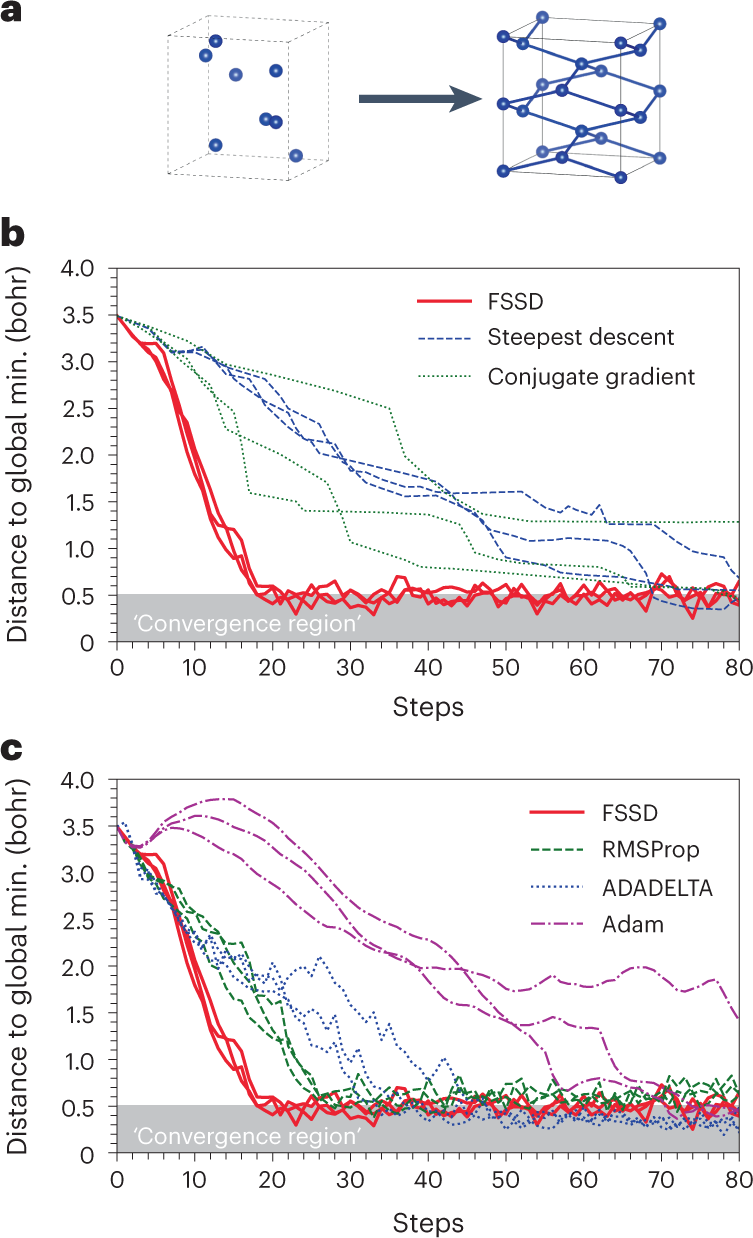
A structural optimization algorithm with stochastic forces and stresses

Solved 5. Suppose we use the method of steepest descent to
Mathematics, Free Full-Text

Steepest Descent Direction - an overview

convergence divergence - Interpretation of Noise in Function Optimization - Mathematics Stack Exchange
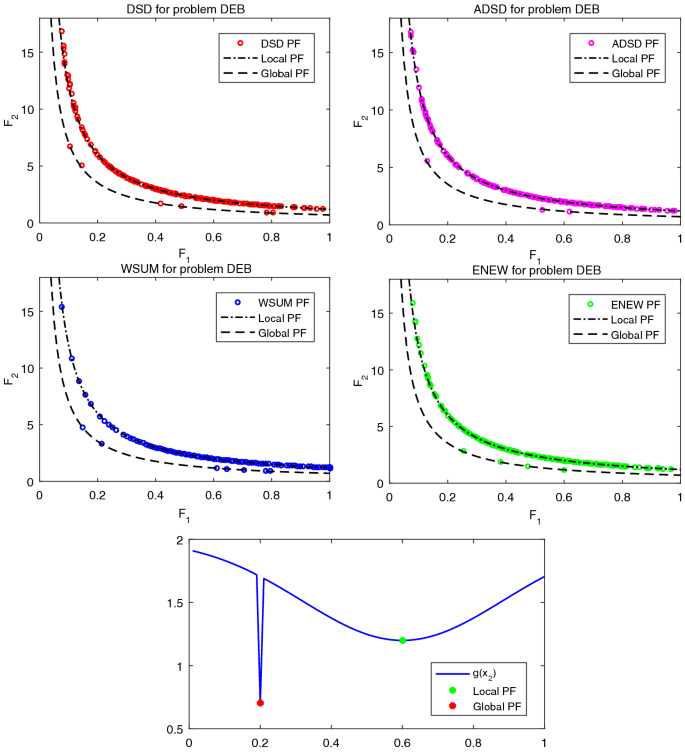
Accelerated Diagonal Steepest Descent Method for Unconstrained Multiobjective Optimization
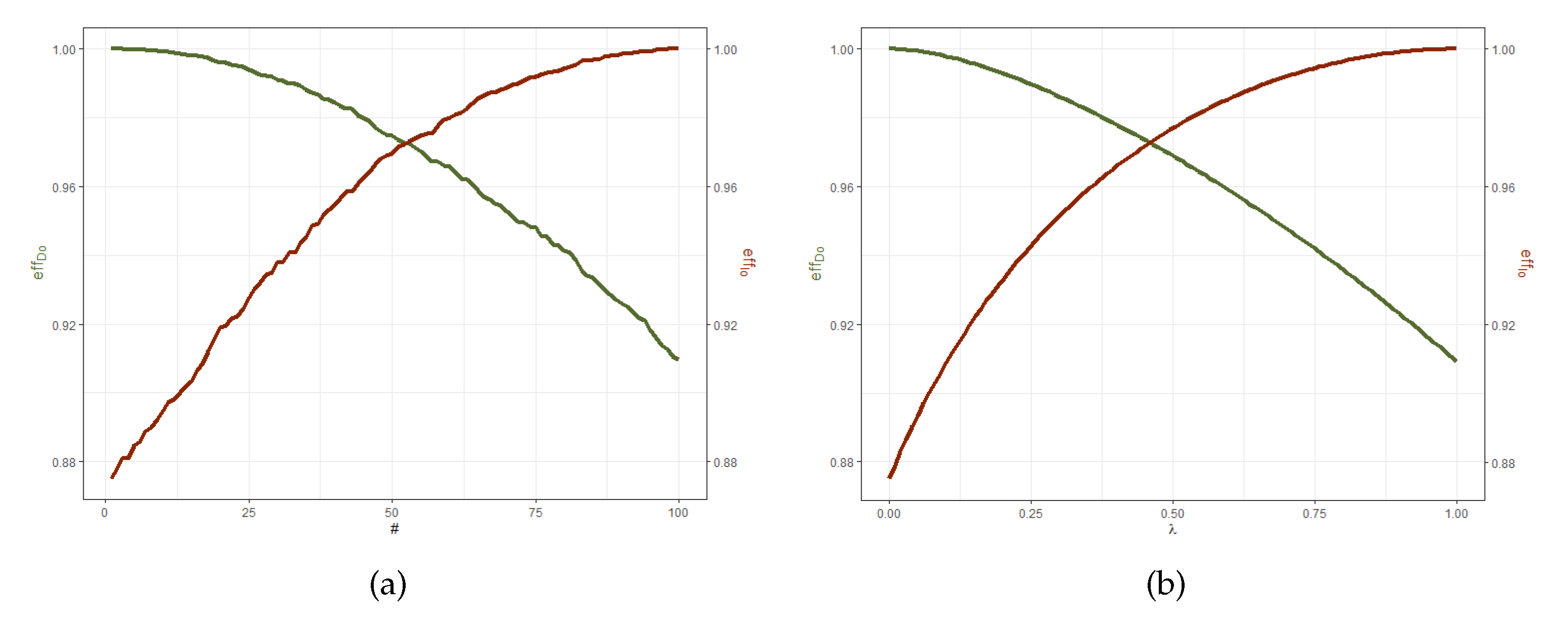
Mathematics, Free Full-Text

Quasi-Newton methods for topology optimization using a level-set method

Reference Request: Introduction to step-size complexity of optimization algorithms - Mathematics Stack Exchange
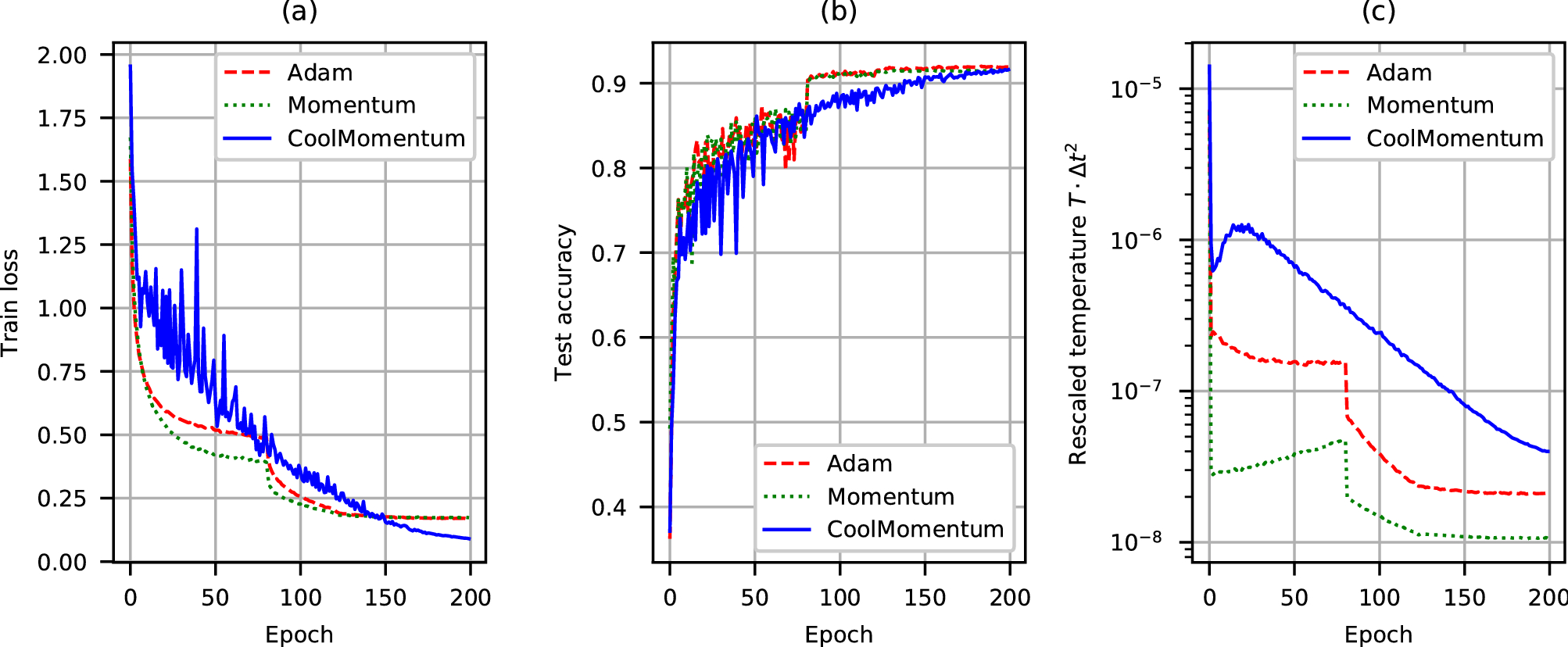
CoolMomentum: a method for stochastic optimization by Langevin dynamics with simulated annealing
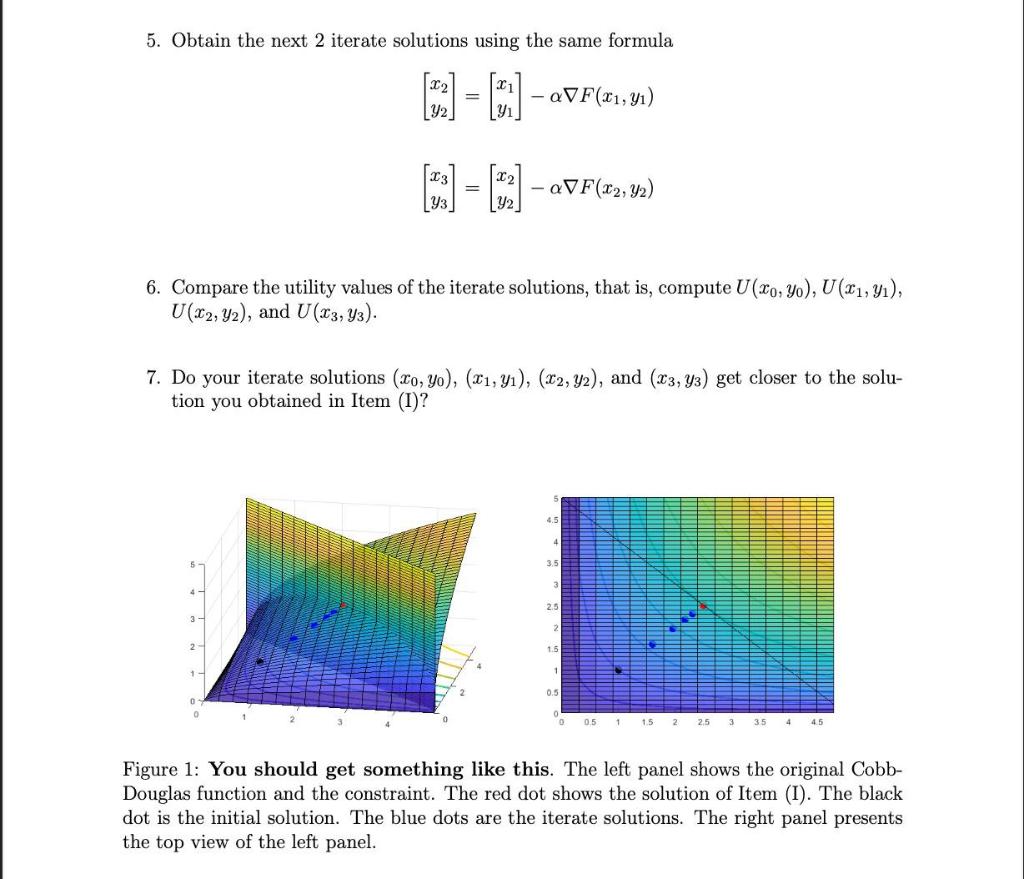
Solved I. Solve the following utility maximization problem
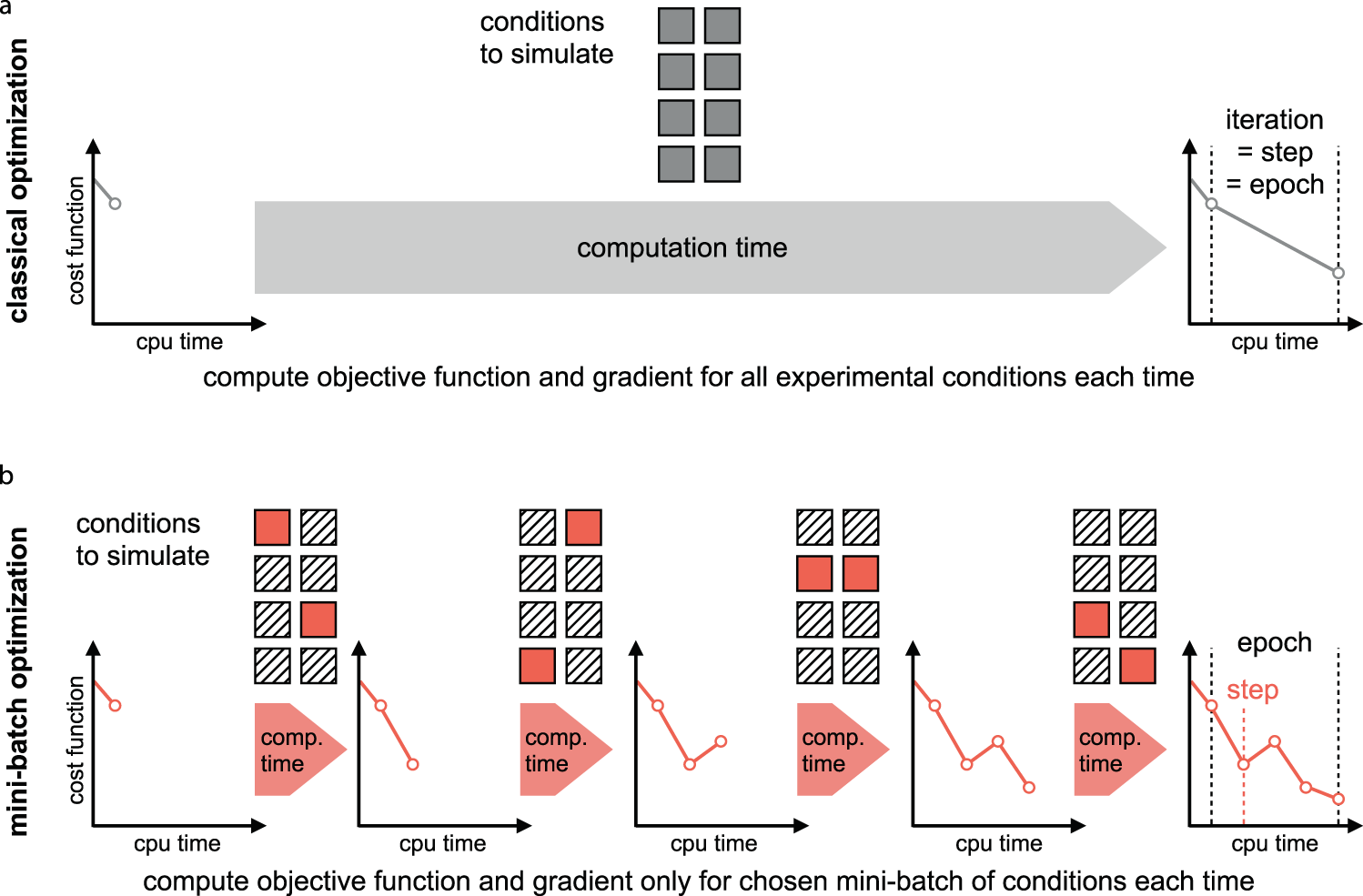
Mini-batch optimization enables training of ODE models on large-scale datasets
de
por adulto (o preço varia de acordo com o tamanho do grupo)