Casa
strangers to friends

Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers

Por um escritor misterioso

Descrição
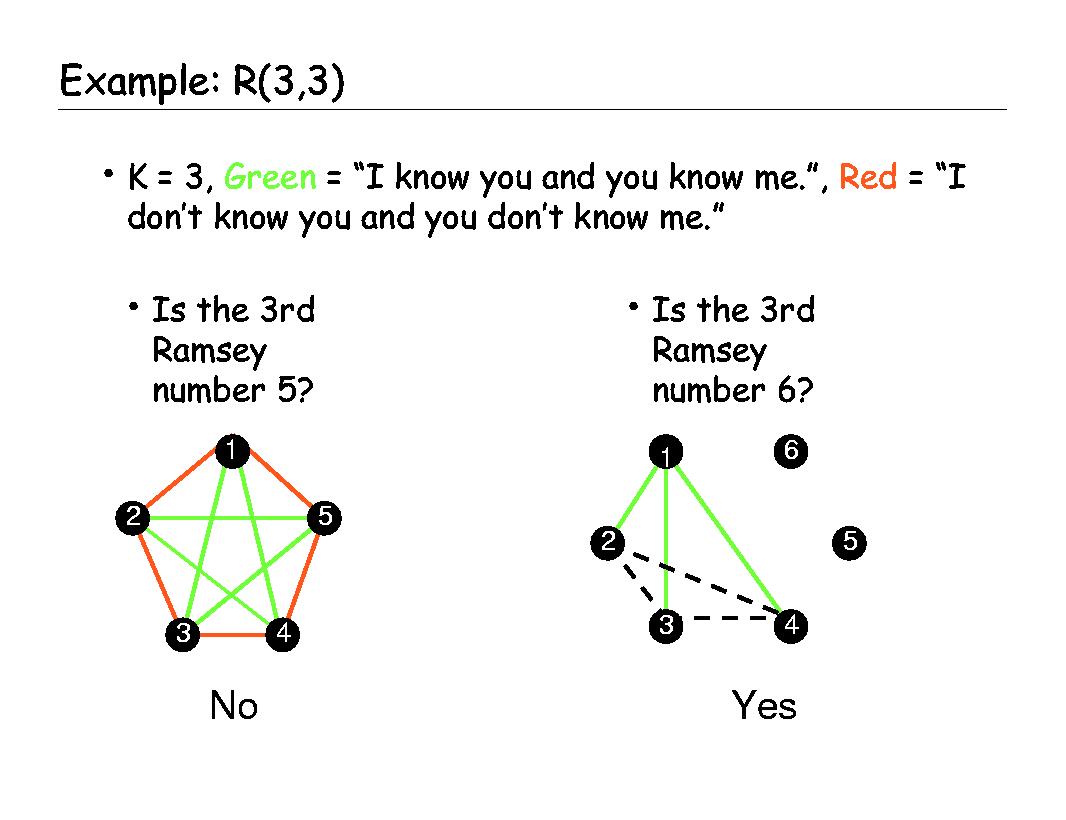
Let’s take a look at Alice first. To her, each one of the other five (Bob, Carol, Dave, Ellen, and Frank) is either a friend or a stranger. Suppose Bob, Dave, and Frank are friends to Alice, and…
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Correlation, Causation, and Ramsey Theory
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
CS290I Lecture notes -- Let's Party
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on friends and strangers - Wikipedia
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
This math puzzle will help you plan your next party
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on Friends and Strangers. Ramsey Theory and Graham's Number, by Francesco Di Lallo
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Materials, Free Full-Text
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
SOLVED: Prove this theorem: Among any six people, there exists a group of 3 mutual friends or a group of 3 mutual strangers. (Here friends and strangers are considered symmetric relations, i.e.
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
How to prove: at a party of six people either there are three mutual acquaintances or there are three mutual strangers - Quora
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on Friends and Strangers. Ramsey Theory and Graham's Number, by Francesco Di Lallo
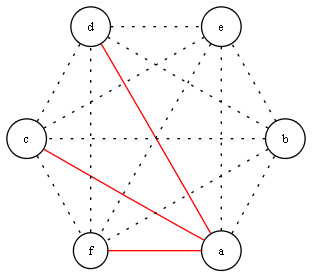
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and Strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Solved Counting: product rule, sum rule, inclusion-exclusion
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Correlation, Causation, and Ramsey Theory
de por adulto (o preço varia de acordo com o tamanho do grupo)